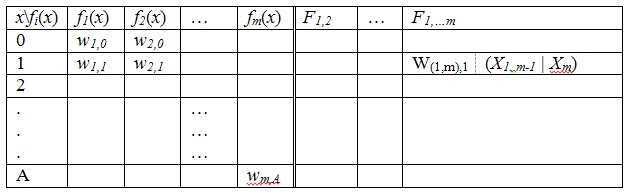
В предыдущем посте я представлял схему имитационного моделирования для оптимизации распределения ресурсов в условиях неопределенности. В этой статье покажу приложение, которое я написал для решение этой задачи.

Данная программа предназначена для решения задач оптимизации распределения ресурсов при неполной информации с применением методов имитационного моделирования.

Ограничений на количество ресурсов и пунктов назначения теоретически нет, так как программа работает с динамической памятью. Реальный предел зависит от количества памяти и операционной системы.

Кроме того, в программе реализовано:

1. Сохранение и загрузка задач во внешний файл.
2. Каждый эффект от вложения определенного количества ресурса в определенный пункт может быть как статическим так и случайной величиной, лежащей в определенном диапазоне и распределенной по выбранному закону распределения.
3. Использование 5 различных законов распределения:

• Равномерный
• Нормальный
• Экспоненциальный
• Вид возрастающего треугольника
• Вид убывающего треугольника

1. Тестирование датчиков случайных чисел на тождественность теоретического закона ‑ эмпирическому, по критерию Колмогорова
2. Проведение имитационного моделирования задачи с неполной информацией, при этом реализован вывод следующих данных:

• График плотности распределения значений эффективности за последний этап итераций
• График функции распределения значений эффективности за последний этап итераций
• Оценка соответствия полученного распределения эффективностей нормальному закону,  по критерию Колмогорова
• Вывод среднего значения эффективности за последний этап итераций
• Вывод среднеквадратического отклонения от среднего за последний этап итераций
• Вывод моды за последний этап итераций
• Построение доверительного интервала
• Вычисление вероятности попадания в доверительный интервал
• Вывод уникальных,  перспективных вариантов решения задачи, попадающих в доверительный интервал
• Построение графика стремления к устойчивому состоянию и указания 5% и 2% коридора
• Проверка неравенства Чебышева и вычисления необходимого числа итераций от допустимой ошибки

Программа имеет не сложный, но в то же время достаточно функциональный и удобный в применении интерфейс, позволяющий выполнять достаточно много операций для исследования и анализа результатов решения.

Читать далее

Задачи оптимизации распределения ресурсов при неполной информации встречаются в различных областях человеческой деятельности, потому что часто приходится решать такие задачи, где из некоторого набора вариантов решения нужно выбрать наиболее перспективные, удовлетворяющие определенным требованиям.

С такими проблемами специалисты-практики сталкиваются, решая, например,  экономические, производственные и другие задачи, т.е. везде, где есть некоторое количество ресурсов, пунктов потребления этих ресурсов и сведения об эффективности от вложения ресурсов в определенные пункты.

Например, задача распределения ресурсов в производстве может иметь следующую формулировку. Имеется несколько различных катализаторов производственного процесса, стадии этого процесса и экспериментальные данные об эффекте, получаемом от вложения катализаторов. Нужно конкретное количество распределить по стадиям так, чтобы максимизировать эффективность производственного процесса, который может выражаться через количество продукции.

В экономической области на место ресурсов становятся денежные средства, на место пунктов вложения ‑ либо города, в которые вкладывают средства, либо сфера деятельности, либо конкретный товар. Эффективностью вложения при этом можно называть прибыль, получаемую от вложения средств.

Задача эксперта состоит в том, чтобы исследовать зависимость решения задачи от исходных данных. На основании набора экспериментальных данных он исследует и анализирует  работу системы, и выбирает наиболее перспективные и максимально эффективные варианты решения задачи для того, чтобы их предоставить заказчику.

В условиях неполной информации эксперту предстоит изучать и анализировать систему. Для проведения многократных экспериментов необходимо имитировать реальную систему. Этот процесс называется имитационным моделированием.

Под имитацией системы понимается организация эксперимента, обеспечивающего логическую взаимосвязь свойств модели в соответствии с реальностью изучаемого процесса. Результаты имитации дополняют неполную информацию о начальных состояниях системы и ее входных воздействиях.

Читать далее