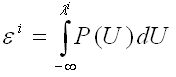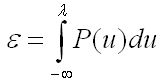PDF

Известно, что в языках программирования встроен генератор случайных чисел. Обычно он генерирует значения от 0 до 1 по равномерному закону распределения. Иногда необходим генератор, который генерировал бы числа по другому закону распределения, например, по нормальному закону распределения, экспоненциальному или какому-либо другому.

В основе построения датчиков случайных величин лежит утверждение:

где

ε – случайная величина, принадлежащая промежутку [0..1], и имеющая равномерный закон распределения.

P(U) – требуемый закон распределения

Для того, чтобы вывести формулу датчика случайных чисел, с требуемым законом распределения, необходимо проинтегрировать требуемый закон плотности вероятности в аналитическом виде с заданными пределами.

Площадь фигуры под функцией плотности распределения в пределах от  до  должна равняться 1:

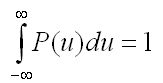
После интегрирования необходимо выразить λ(СВ с требуемым законом) через ε(СВ с равномерным законом).

Далее можно воспользоваться критерием Колмогорова, чтобы проверить тождественность теоретического закона и эмпирического, чтобы оценить, можно ли пользоваться выведенной формулой закона распределения.

Для проверки критерия Колмогорова необходимо знать максимальную разницу между функциями распределения случайных величин теоретического и эмпирического закона. Учитывая, что плотность распределения случайной величины – это производная функции распределения случайной величины, функцию распределения не трудно найти:

f(x) = F’(x)

где

f(x) – плотность распределения

F(x) – функция распределения

Критерий Колмогорова:

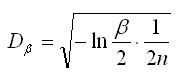
где

β – уровень значимости (обычно равен 0.05)

n – количество значений в выборке

Если величина D_β больше максимального расхождения между функциями распределения теоретического и эмпирического закона случайных величин, то формулой эмпирического закона можно пользоваться.

Таким образом , были получены формулы для генерации случайных чисел в заданном диапазоне (a..b) по равномерному, нормальному, экспоненциальному, по закону y=x и y=-x.  Последние два похожи на прямоугольные треугольники, один со стороной y=x, а другой y=-x.

var d: real;

d := b - a;

//равномерный:
function TGRVClass.GetRavnomer(): real;
 begin
 Result:=Random*d+a;
end;

//нормальный:
function TGRVClass.GetNormal(): real;
 begin
 Result:=((Random*d+Random*d+Random*d)/3)+a;
end;

//экспоненциальный:
function TGRVClass.GetExponent(): real;
 begin
 Result:=sqrt(sqrt(Random))*d+a;
end;

//y=x:
function TGRVClass.GetPosibTriangle(): real;
 begin
 Result:=sqrt(Random)*d+a;
end;

//y=-x
function TGRVClass.GetNegativTriangle(): real;
begin
 Result:=(1-sqrt(1-Random))*d+a;
end;

Далее код функций для построения графиков теоретической функции распределения:

//равномерный закон:
function TGRVClass.GetTPlotRavnomer(_x: real): real;
begin
 if (a<=_x) and (_x<=b) then
  begin
    Result:=1/(b-a);
  end
 else
  begin
    Result:=-1;
  end;
end;

//нормальный закон:
function TGRVClass.GetTPlotNormal(_x: real): real;
var
 si, dr, st, M: real;
begin
 if (a<=_x) and (_x<=b) then
  begin
    si:=(b-a)/6;
    M:=(b+a)/2;
    dr:=1/(si*sqrt(2*pi));
    st:=-sqr(_x - M)/(2*si*si);
    Result:=dr*exp(st);
  end
 else
  begin
    Result:=-1;
  end;
end;

//экспоненциальный закон:
function TGRVClass.GetTPlotExponent(_x: real): real;
const
 kf: real = 1.7507867227;
var
 rx: real;
begin
 if (a<=_x) and (_x<=b) then
  begin
    rx:=(_x-a)/(d);
    Result:=(kf*exp(kf*rx)-1)/d;
  end
 else
  begin
    Result:=-1;
  end;
end;

//закон подобный прямой y=x
function TGRVClass.GetTPlotPosibTriangle(_x: real): real;
var
 alf: real;
begin
 if (a<=_x) and (_x<=b) then
  begin
   alf:=2/(b-a);
   Result:=alf*(_x-a)/(b-a);
  end
 else
  begin
   Result:=-1;
  end;
end;

//закон подобный прямой y=-x:
function TGRVClass.GetTPlotNegativTriangle(_x: real): real;
var
 alf: real;
begin
 if (a<=_x) and (_x<=b) then
  begin
   alf:=2/(b-a);
   Result:=alf-alf*((_x-a)/(b-a));
  end
 else
  begin
   Result:=-1;
  end;
end;

Вот, что получается на графиках с различными выборками.

В окне предусмотрена область для ввода исходной информации необходимой для построения, и оценки функции распределения, плотности вероятностей и коэффициента размытости. От пользователя требуется ввести количество элементов выборки, диапазон значений СВ, закон распределения и тип ядерной функции для построения графиков. С помощью флажка Просмотр действий можно включить просмотр вычислений в реальном времени, однако, данный режим замедляет вычисления.

Для оценки тождественности теоретического закона распределения эмпирическому существует настраиваемый параметр Уровень значимости.

После щелчка на кнопке Рассчитать строятся графики функции и плотности распределения теоретического закона и эмпирического.

Например, так выглядит график плотности распределения случайной величины распределенной по равномерному закону при выборке 100 значений в диапазоне от 0 до 1.

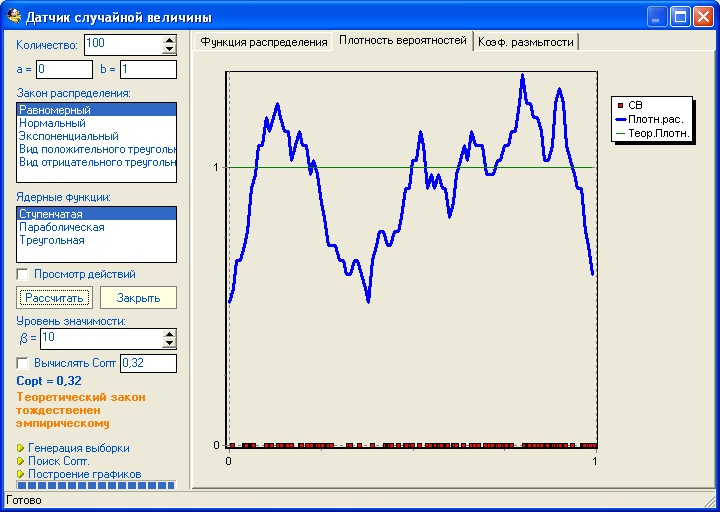
Несмотря на том, что график слабо похож на теоретический закон, по критерию Колмогорова при уровне значимости в 10% законы тождественны.

При 1000 значений он уже близок к теоретическому:

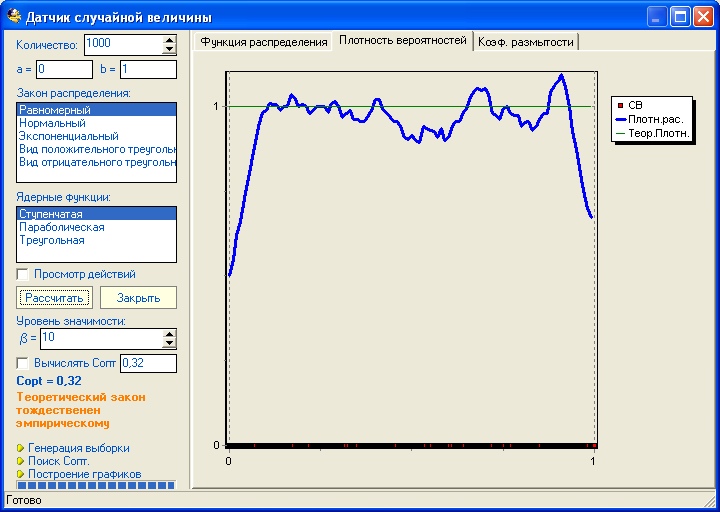
Теперь, например, график плотности распределения случайной величины распределенной по нормальному закону с количеством значений в выборке равному 100:

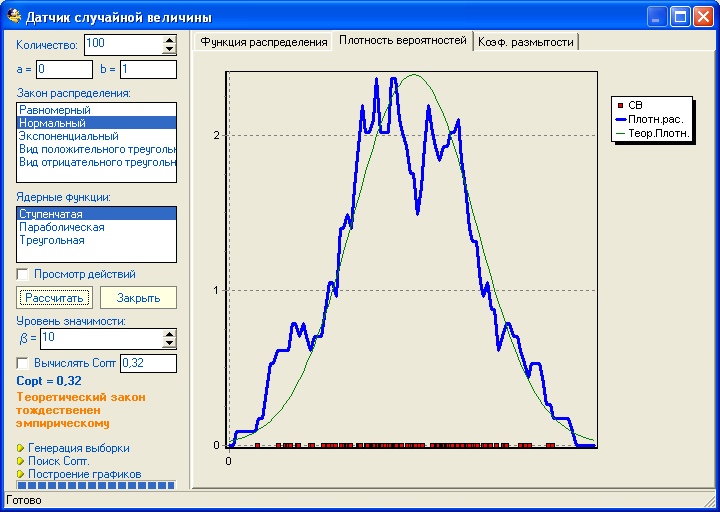
При 10000 значений график весьма близок к теоретическому:

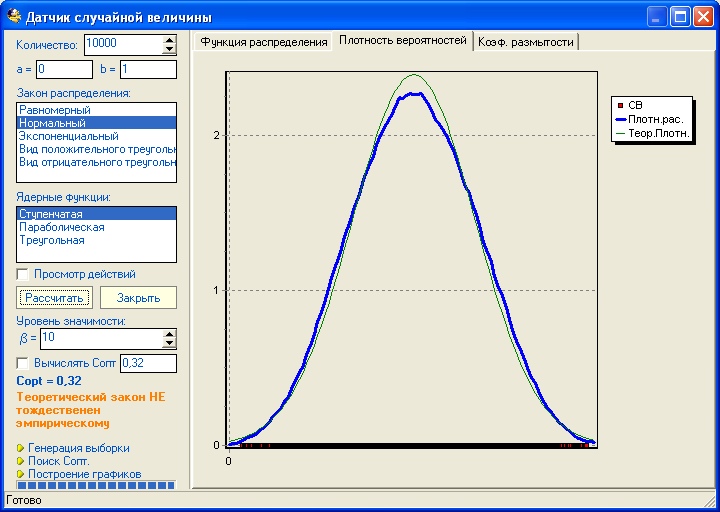
Данный генератор потребовался для проекта имитационного моделирования решения задачи распределения ресурсов в условиях неопределенности. Об этом напишу в следующий раз.